Recursos especiales de Pascua 🐰 

Guía en formato word editable de historia y geografía "Plano". Ideal para trabajar en primer ciclo (segundo a cuarto año básico) Contiene:
-Información y/o explicación del contenido a trabajar.
-Reconocer simbología del plano de una habitación, ubicando objetos y nombres.
-Dibujar y crear plano de una sala de clases con simbología dada.

Guía en formato word editable de matemática "Composición y descomposición aditiva hasta 1000" tercer año. Contiene:
-Explicación del contenido a trabajar.
-Ubicar y dibujar objetos según coordenadas dadas.
-Comprender plano con coordenadas.
-Responder de acuerdo a plano con coordenadas dadas.

Recurso de contenido e información que sirve de base para la electividad de Artes visuales, audiovisual y multimediales. Además es transversal para cuando quieras solicitar un trabajo relacionado a lo audiovisual.

📸 Descubriendo los Planos Fotográficos 🎬
Los planos fotográficos son como las notas en una partitura musical, combinándose para crear una melodía visual que cautiva nuestros sentidos y despierta nuestra imaginación. Desde el amplio panorama de un plano general 🌍 hasta el detalle íntimo de un primer plano extremo 👁️, cada plano tiene el poder de comunicar emociones, contar historias y transportar al espectador a mundos imaginarios. Comprender estos planos no solo es esencial para los fotógrafos y cineastas, sino también para cualquier persona interesada en el arte visual.

Al entender cómo cada plano afecta la percepción del espectador y contribuye a la narrativa visual, podemos expresar ideas, emociones y narrativas de manera más impactante y coherente en nuestras propias obras 🖼️. Además, al analizar y apreciar el trabajo de otros artistas visuales, podemos enriquecer nuestra comprensión del arte fotográfico y cinematográfico 🎨.

En resumen, dominar los planos fotográficos no solo nos brinda las herramientas necesarias para la comunicación efectiva y la expresión creativa en la fotografía y el cine, sino que también nos permite apreciar más profundamente el arte visual en todas sus formas 🌟.

En este recurso encontrarás un archivo PDF con los planos fotográficos. Sin embargo puedes adecuar a tus necesidades y a las de tus estudiantes para seguir complementando el material. 

No olvides dejar tu reseña o comentario para seguir mejorando nuestros recursos.

Evaluación de matemática quinto año básico en formato word editable, unidad 5: "Geometría". Contiene los siguientes objetivos:

• Clasificar distintos tipos de rectas, polígonos y poliedros.
• Reconocer posiciones relativas de lados en figuras geométricas.
• Reconocer posiciones relativas de aristas y caras en cuerpos geométricos.
• Ubicar puntos y figuras en el plano cartesiano.
• Aplicar transformaciones isométricas a distintas figuras en el plano cartesiano.
• Comprender el concepto de congruencia.

La prueba contiene 30 preguntas las cuales son de selección múltiple y  además contiene una pregunta de desarrollo .

El objetivo de esta guía es poder trabajar la ubicación con los puntos cardinales dentro de un plano. 
El alumno debe comprender que cada cosa/persona tiene una ubicación dentro del plano que puede describir con los puntos cardinales.

Esta presentación está diseñada como una herramienta pedagógica interactiva para enseñar de manera clara y sencilla la ubicación de puntos y figuras en el plano cartesiano. Se estructura en pasos secuenciales que permiten al estudiante comprender gradualmente los conceptos básicos y avanzar hacia aplicaciones prácticas.

Conocer los elementos básicos de la geometría, como el punto, la recta, el plano, la línea, el segmento de recta y el rayo o semirrecta, es fundamental para comprender y describir el espacio que nos rodea. Estos conceptos son la base para el estudio de formas y figuras, facilitando la resolución de problemas cotidianos y complejos en diversas áreas como la arquitectura, la ingeniería y el diseño. Además, la geometría desarrolla habilidades de razonamiento lógico y visualización espacial, esenciales para el aprendizaje de las matemáticas y otras ciencias. Dominar estos elementos es clave para un pensamiento crítico y creativo.

 | OBJETIVO(S) DE LA CLASE
| ·         Resolver prueba formativa.  

 

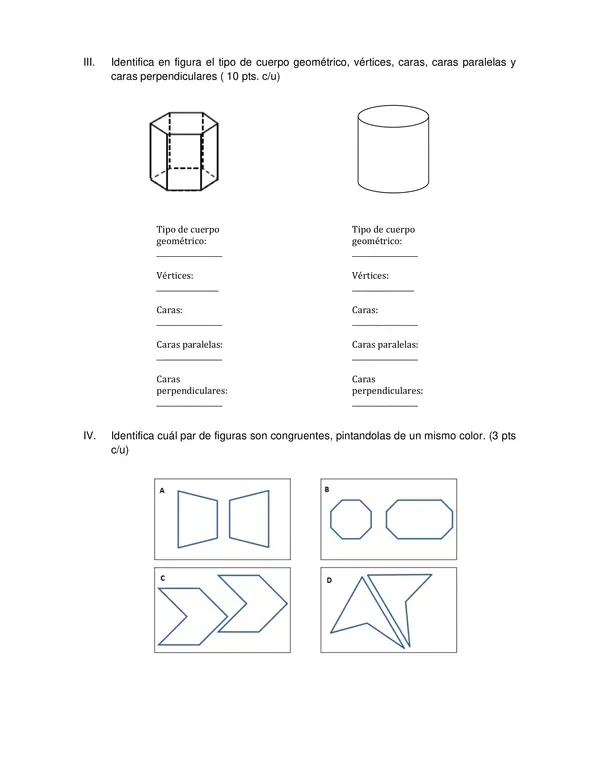
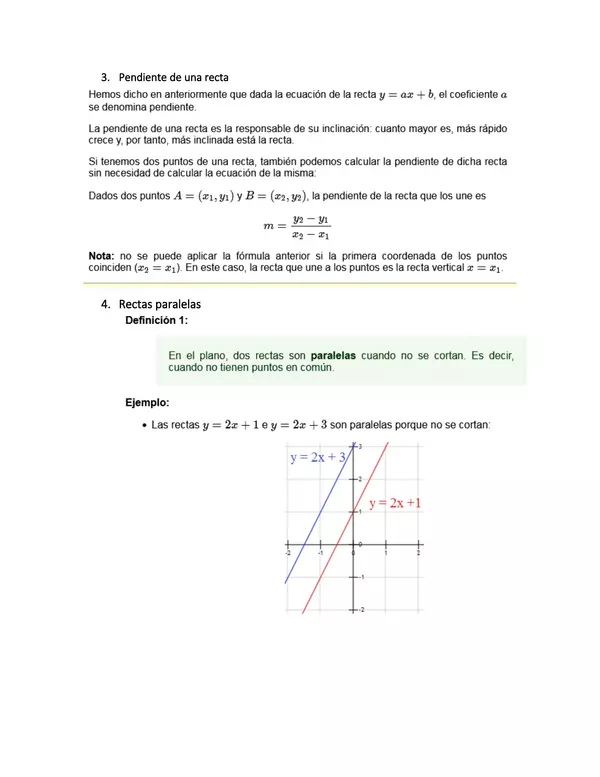
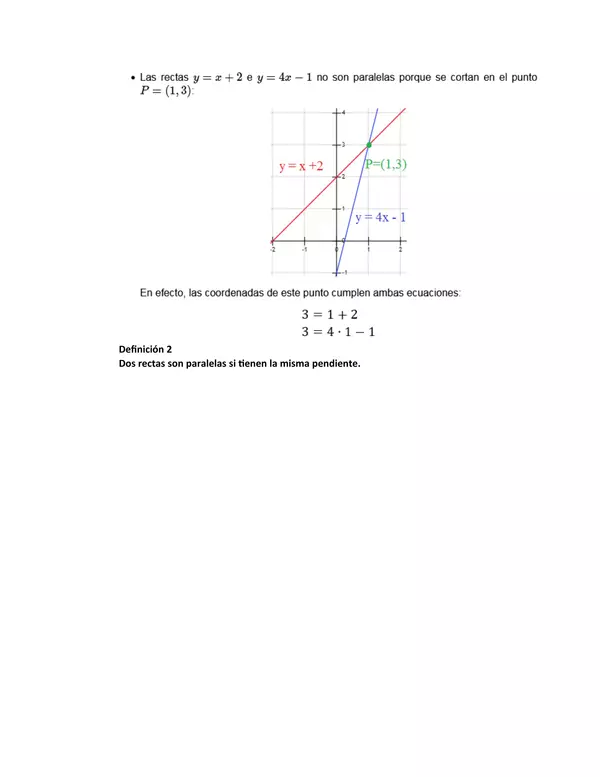
 | Objetivo(s) de Aprendizaje: | ·         Identificar y dibujar puntos en el primer cuadrante del plano cartesiano, dadas sus coordenadas en números naturales. (OA 16) ·         Describir y dar ejemplos de aristas y caras de ¬figuras 3D, y lados de -figuras 2D: ·         que son paralelos. ·         que se intersectan. ·         que son perpendiculares. (OA 17) ·         Demostrar que comprende el concepto de congruencia, usando la traslación, la reflexión y la rotación en cuadrículas. (OA 18)   
| Actitudes: | ·         Manifestar un estilo de trabajo ordenado y metódico. ·         Abordar de manera flexible y creativa la búsqueda de soluciones a problemas. ·         Demostrar una actitud de esfuerzo y perseverancia. 
| Habilidades:   | ·         Comunicar de manera escrita y verbal razonamientos matemáticos: describiendo los procedimientos utilizados, usando los términos matemáticos pertinentes (OA f). ·         Extraer información del entorno y representarla matemáticamente en diagramas, tablas y gráficos, interpretando los datos extraídos (OA l). ·         Usar representaciones y estrategias para comprender mejor problemas e información matemática (OA m). ·         Imaginar una situación y expresarla por medio de modelos matemáticos (OA n).  

______________________________________________________________________________________

Inicio: 

·         El profesor da a conocer las indicaciones y el objetivo de la evaluación. 

·         El profesor da una instancia para que se formen grupos de a lo más tres personas, eligiendo dentro de ellos un representante. 

·         El docente en conjunto con los estudiantes, realizan resumen de la clase, destacando los principales conceptos aprendidos durante la unidad, de tal modo que se definan, conecten y apliquen en diversos contextos.   

·         El profesor entrega a cada integrante de los grupos la evaluación formativa. 

·         El profesor monitorea el desarrollo de la actividad de modo de ir aclarando dudas e inquietudes presentes en su desarrollo. 

·         Se solicita a cada uno de los representantes que salgan a la pizarra a resolver los ejercicios que el docente les indique, de modo de ir revisando en conjunto con los estudiantes el desarrollo de la actividad, fomentado el trabajo colaborativo.   

·         El docente destaca los principales errores cometidos por los estudiantes. (Observados en el monitoreo de la actividad)  para que no sean cometidos en la evaluación sumativa. 

·         El docente vuelve a destacar cada uno de los conceptos aplicados en la evaluación, recordando que serán evaluados en la prueba de unidad (Patrón numérico, sucesión, tabla de doble entrada, ecuación lineal con una incógnita).    

Contenidos 

Geometría Analitica - Nivel Básico

1. Introducción
2. Recordatorio
3. Rectas paralelas
4. Rectas perpendiculares
5. Problemas Resuelto

Nota :

Los conceptos de rectas paralelas y de rectas perpendiculares (nivel de secundaria). Para poder comprender y resolver los problemas, el alumno necesitará tener las siguientes destrezas:Saber interpretar o representar en el plano la gráfica de una recta.Saber encontrar la ecuación de la recta que pasa por dos puntos.Resolver ecuaciones de primer grado.

Se sugiere que el estudiante se familiarice con las herramientas de construcción gráfica de Gogebra.