Evaluación semestral de matemática primer semestre, cuarto año básico. Contiene:
-Números hasta 10 000 
-Lectura y escritura de números hasta 10 000
- Resolver ejercicios y problemas de adición y sustracción de números
- Resolver área y volumen de figuras  2D y 3D
- Ordenar cantidades en recta numérica.
-Reconocer patrones y secuencias numéricas.
-Identificar valor posicional U, D, C y UM 
-Ordenar y formar números
-Resolver problema de valor monetario 
-Ejercicios de medición cm y metro.
-Ubicar objetos en cuadrícula.
-Reconocer y medir ángulos
-Trazar ejes de simetría
-Realizar  rotación de dibujos 
-Reconocer hora 
-Dibujar vistas de figuras 3D

conocer las formulas más utilizadas en las primeras clases de gastronomía, recordarlas para ir aplicándola a diferentes actividades de planificación de menú y carta, de esta forma podrán calcular cantidades necesarias para elaborar lo solicitado y cuantificar los costos

Este proyecto consiste en que los estudiantes deben crear su propia pastelería y por medio de esto trabajar fracciones y decimales.

Incluye:

- una página en la que los estudiantes puedes ser creativos y pensar el nombre, el slogan y el logo de su pastelería

- 6 páginas para calcular recetas (multiplicación y división de fracciones)

- 1 página para calcular cantidades (suma de fracciones)

- 2 páginas para comparar precios (comparar decimales) 

- 3 páginas con problemas mixtos de decimales

- 2 páginas con problemas mixtos de fracciones

Además se incluye una plantilla en blanco a disposición del profesor por si quiere añadir otro tipo de problemas.

Todos los textos son editables y puedes hacerle las modificaciones que consideres importantes y necesarias para tus estudiantes.

De igual manera puedes borrar las páginas que no deseas trabajar, si deseas que el proyecto sea más corto o algunos de los problemas te parecen no adecuados para tus estudiantes.

Este proyecto consiste en que los estudiantes deben crear su propia pastelería y por medio de esto trabajar fracciones y decimales.

Incluye:

- una página en la que los estudiantes puedes ser creativos y pensar el nombre, el slogan y el logo de su pastelería

- 6 páginas para calcular recetas (multiplicación y división de fracciones)

- 1 página para calcular cantidades (suma de fracciones)

- 2 páginas para comparar precios (comparar decimales) 

- 3 páginas con problemas mixtos de decimales

- 2 páginas con problemas mixtos de fracciones

Además se incluye una plantilla en blanco a disposición del profesor por si quiere añadir otro tipo de problemas.

Todos los textos son editables y puedes hacerle las modificaciones que consideres importantes y necesarias para tus estudiantes.

De igual manera puedes borrar las páginas que no deseas trabajar, si deseas que el proyecto sea más corto o algunos de los problemas te parecen no adecuados para tus estudiantes.

Estimar el área de un círculo es crucial en muchas aplicaciones prácticas, como en la construcción, diseño y ciencia. Permite calcular la cantidad de material necesario para cubrir superficies circulares, como pisos o techos. Además, es fundamental para analizar problemas en física y matemáticas, como la distribución de fuerzas o la eficiencia de diseños. Entender cómo estimar el área ayuda a tomar decisiones informadas y optimizar recursos, haciendo que el cálculo preciso sea esencial en diversas disciplinas.

Resolver problemas sobre el área y perímetro de círculos es crucial en matemáticas, ya que permite aplicar conceptos fundamentales en diversas áreas como la ingeniería, arquitectura y diseño. Identificar círculos como lugares geométricos ayuda a entender sus propiedades y resolver problemas prácticos, como calcular la cantidad de material necesario para cubrir superficies redondas o el espacio disponible en un diseño. Estas habilidades son esenciales para desarrollar una sólida comprensión matemática y para aplicar soluciones efectivas en situaciones del mundo real.

 Curso                                                          :         Cuarto Año Básico 

Unidad                                                      :  2. Números y formas en el entorno. 

 | OBJETIVO(S) DE LA CLASE
| ü  Aplicar estrategias de cálculo mental y explicarlas. ·         Resolver situaciones de reparto y explica la solución.

 

 | Objetivo(s) de Aprendizaje: | ·         Describir y aplicar estrategias de cálculo mental  conteo hacia delante y atrás , doblar y dividir por 2, por descomposición y usar el doble del doble para determinar las multiplicaciones hasta 10x10 y sus divisiones correspondientes  (OA 2) ·         Demostrar que comprende la división con dividendos de dos dígitos y divisores de un dígito: usando estrategias para dividir con o sin material concreto, utilizando la relación que existe entre la división y la multiplicación, estimando el cociente, aplicando la estrategia por descomposición del dividendo  y aplicando el algoritmo de la división (OA 6))
| Actitudes: | ·         Demostrar una actitud de esfuerzo y perseverancia.)
| Habilidades:   | ·         Resolver problemas dados o creados (OA a) ·         Transferir una situación de un nivel de representación a otro (por ejemplo: de lo concreto a lo pictórico y de lo pictórico a lo simbólico, y viceversa) (OA n))

______________________________________________________________________________________ 

Inicio: 

·         El docente saluda cordialmente a la clase 

·         Se mencionan las normas de trabajo en el aula y de cuidado con el material si procede. 

·         Se da a conocer el objetivo de la clase. 

Desarrollo: 

·         Se entrega  la guía y si es posible se proyecta a toda la clase. 

·         Se desarrolla ítem por ítem y se va revisando en conjunto. 

·         Los estudiantes pasan a la pizarra a completar las actividades de la guía para revisión. 

·         No se puede avanzar al ítem siguiente sin revisar en conjunto el ítem anterior. 

·         Se debe dar tiempo para la comunicación y argumentación de ideas y/o estrategias. 

·         Se proyecta el PowerPoint Clase N°1. Diapositiva 1: Se habla sobre la repostería, ¿de qué se trata?, ¿qué cosas hace un/a repostero/a?, ¿qué ingredientes usa?, etc. 

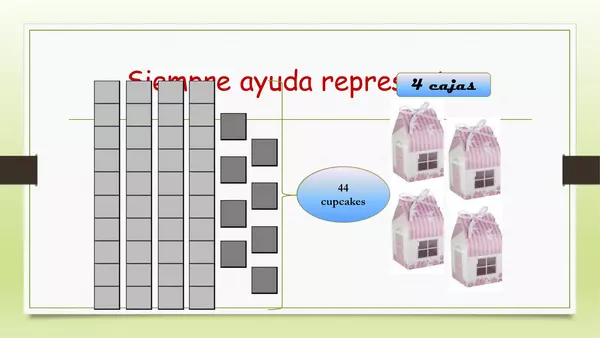
·         Diapositiva 2: Se presenta la situación de Paula, se les da tiempo para resolver la situación sin darle ninguna pista, se les permite comunicar sus ideas y resultados. 

·         Diapositiva 3: Se representa la cantidad con el material (se entrega el material a los estudiantes), ¿cómo nos ayuda esta representación?, ¿cómo podríamos calcular la cantidad de cupcakes en cada caja? 

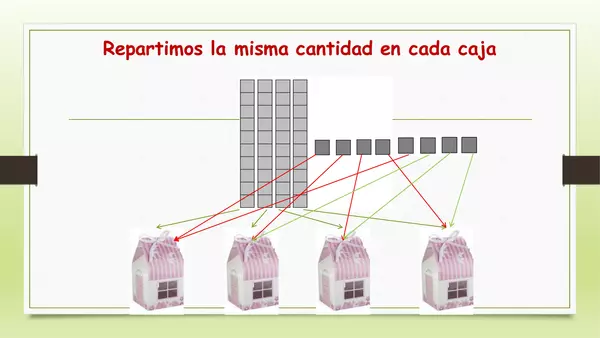
·         Se les da tiempo para resolver la situación y obtener el cociente haciendo repartos, aún no se llama división ni se presentan sus términos (divisor, dividendo, cociente). 

·         Es importante que a medida que aparecen los resultados los vayan identificando en las tablas de multiplicar, e ir viendo si esto sucede cada vez que se usan las tablas. 

·         ¿Qué hicimos hoy? (se escucha el resumen de la clase por parte de los estudiantes) 

·         Se realizan las preguntas o comentarios que se crean necesarios según los acontecimientos sucedidos durante la clase 

·         ¿Cuál era el objetivo de la clase? 

·         ¿Lo conseguimos? ¿por qué? Se dan ejemplos. 

 |  

Otro(s) Indicador(es) de Calidad: 

·       Autoestima académica y motivación escolar: el/la docente refuerza positivamente al grupo curso por manifestar interés genuino durante la clase, invitándoles además a continuar esforzándose por su aprendizaje en diversos ámbitos de sus vidas. 

Recomendaciones: 

ü  Es importante dar tiempo a los estudiantes para que comuniquen sus ideas, sin apurarlos, sin interrumpirlos y sin invalidar sus ideas y/o procedimientos errados, sino aprovechando el error como oportunidad de aprendizaje. 

Materiales / Recursos: 

·       Impresión de la guía del estudiante 

·       Proyección PowerPoint adjunto 

Las cuatro operaciones básicas (suma, resta, multiplicación y división) son fundamentales en matemáticas y vida cotidiana. La suma nos permite combinar cantidades y calcular totales, siendo esencial para el manejo del dinero y presupuestos. La resta nos ayuda a encontrar diferencias, calcular cambios y determinar lo que queda después de gastar o usar algo. La multiplicación simplifica sumas repetitivas y es crucial para calcular áreas, volúmenes y proporciones. La división nos permite repartir equitativamente y encontrar promedios o tasas.

Estas operaciones desarrollan el pensamiento lógico y la capacidad de resolución de problemas desde temprana edad. Son la base para conceptos matemáticos más avanzados como álgebra, geometría y cálculo. En el ámbito profesional, permiten realizar análisis financieros, estadísticos y científicos con precisión. También facilitan la comprensión de patrones numéricos y relaciones proporcionales. Sin dominar estas operaciones básicas, sería imposible avanzar en matemáticas superiores o aplicar el razonamiento cuantitativo en situaciones reales del trabajo y la vida diaria.

Las cuatro operaciones básicas (suma, resta, multiplicación y división) son fundamentales en matemáticas y vida cotidiana. La suma nos permite combinar cantidades y calcular totales, siendo esencial para el manejo del dinero y presupuestos. La resta nos ayuda a encontrar diferencias, calcular cambios y determinar lo que queda después de gastar o usar algo. La multiplicación simplifica sumas repetitivas y es crucial para calcular áreas, volúmenes y proporciones. La división nos permite repartir equitativamente y encontrar promedios o tasas.

Estas operaciones desarrollan el pensamiento lógico y la capacidad de resolución de problemas desde temprana edad. Son la base para conceptos matemáticos más avanzados como álgebra, geometría y cálculo. En el ámbito profesional, permiten realizar análisis financieros, estadísticos y científicos con precisión. También facilitan la comprensión de patrones numéricos y relaciones proporcionales. Sin dominar estas operaciones básicas, sería imposible avanzar en matemáticas superiores o aplicar el razonamiento cuantitativo en situaciones reales del trabajo y la vida diaria.