El material presenta una aplicación práctica de las funciones cuadráticas, utilizando el puente Golden Gate como ejemplo. La guía está diseñada para estudiantes de III° medio y tiene como objetivo demostrar cómo las matemáticas, específicamente las funciones cuadráticas, se utilizan en situaciones del mundo real, como la ingeniería de puentes.
-
Introducción a la Aplicación de Funciones Cuadráticas:
-
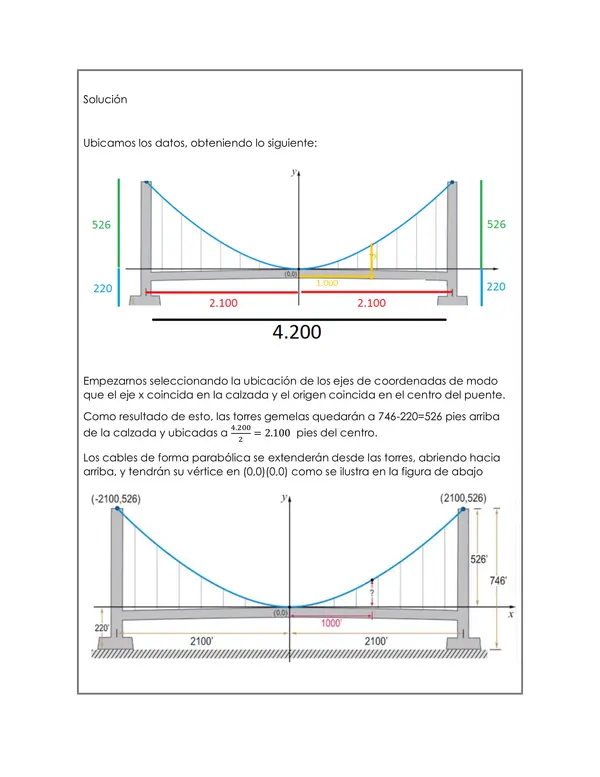
Contextualización: Se describe el puente Golden Gate, resaltando sus dimensiones y la estructura de sus cables suspendidos, que forman una parábola.
-
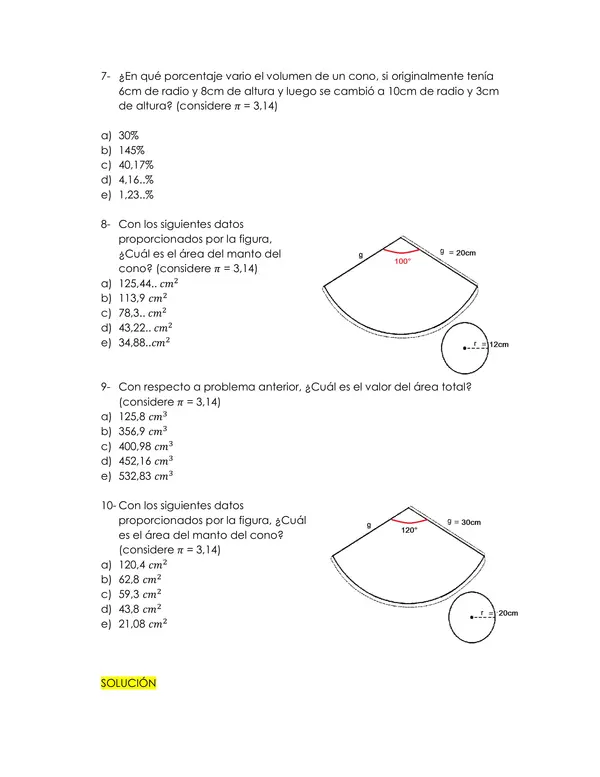
Objetivo: Determinar la altura de los cables a una distancia de 1000 pies del centro del puente.
-
Planteamiento del Problema:
-
Ubicación de Ejes de Coordenadas: Los ejes se colocan de manera
-
Identificación de la Parábola: Cálculo del Valor de
𝑎a:
-
Datos de la Gráfica:
-
Ecuación de la Parábola:
alumno debe leer y comprender la guía, prestando atención a la aplicación de conceptos matemáticos en un contexto real. Luego, debe replicar el ejemplo resuelto para asegurarse de entender cada paso del proceso, desde la colocación de los ejes de coordenadas hasta el cálculo del valor de
𝑎a y la altura del cable a una distancia específica. Posteriormente, el alumno puede formular preguntas al docente para aclarar cualquier duda. Finalmente, se espera que el estudiante aplique el mismo método a problemas similares, reforzando su comprensión de las funciones cuadráticas y su importancia en la resolución de problemas prácticos.














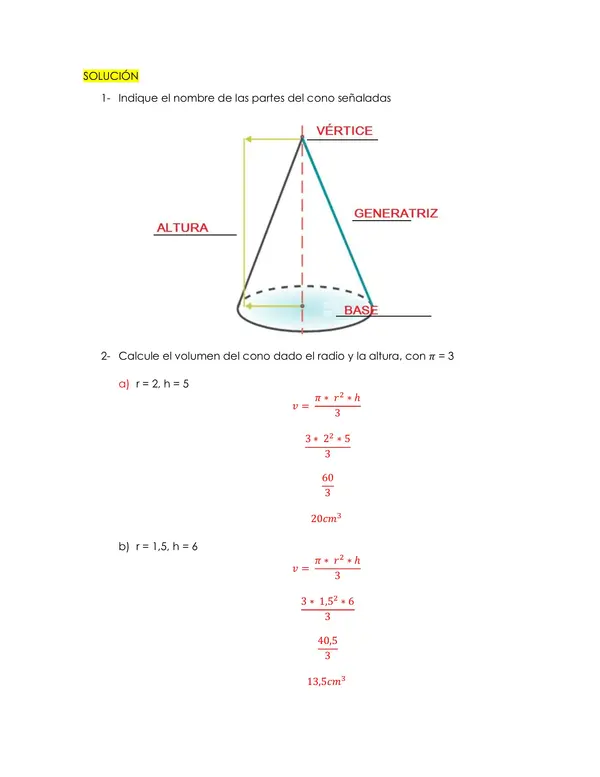








There are no comments yet, write one yourself!