
| Resource type | Worksheet |
| Recommended age | 16 - 18 years |
| File information | pdf, 3 pages, 501 KB |
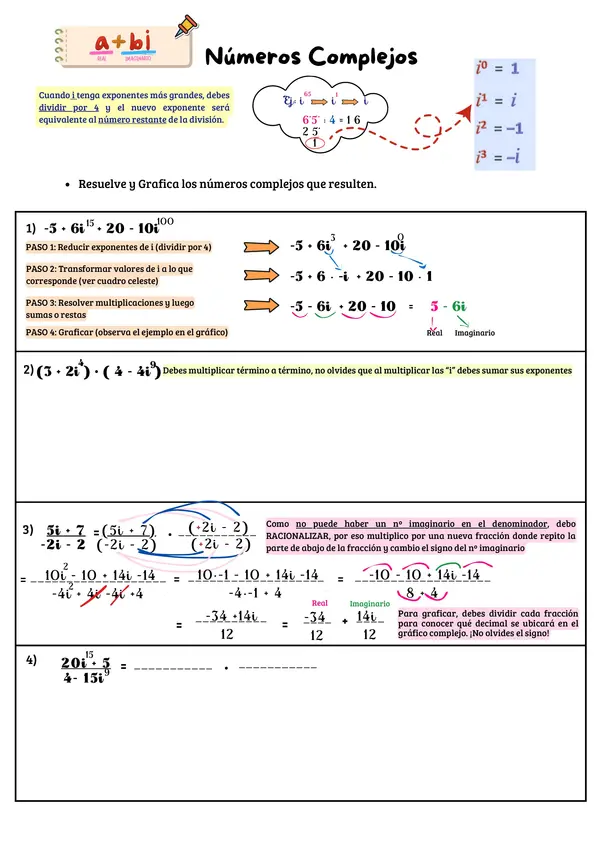
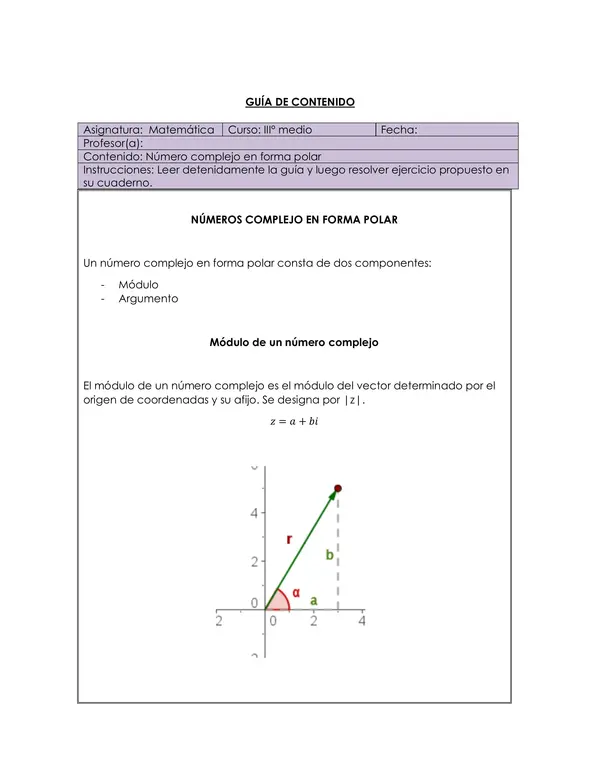
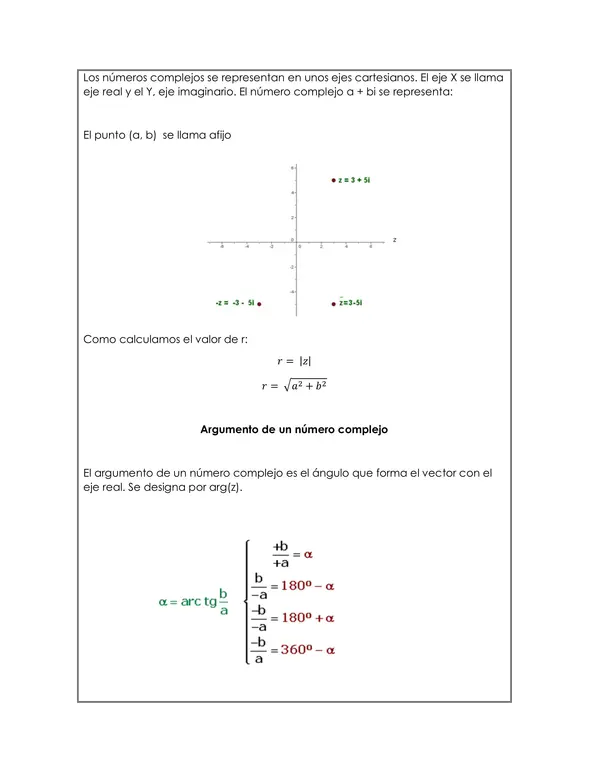
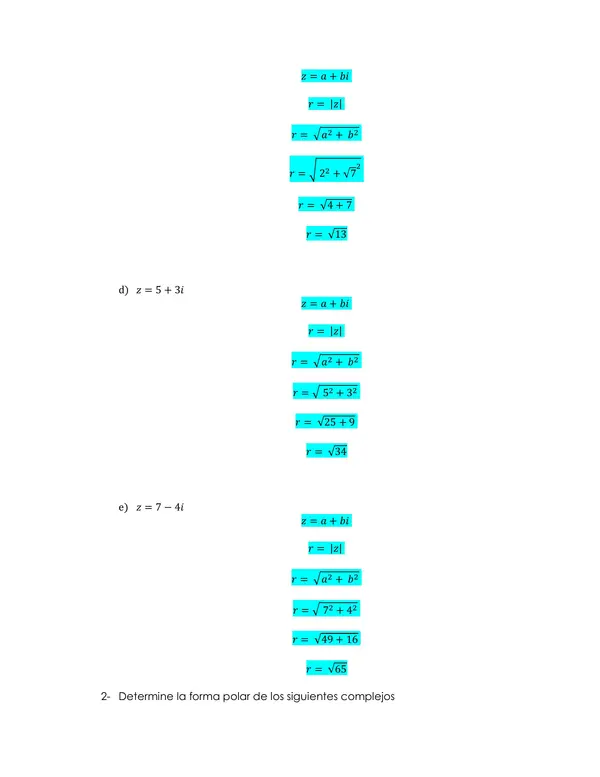
Todo esto con el fin de que el/la estudiante pueda guiarse con los ejemplos y continuar de forma autónoma.


| Resource type | Worksheet |
| Recommended age | 16 - 18 years |
| File information | pdf, 3 pages, 501 KB |
| Downloads count | 3 |
| Resource type | Worksheet |
| Recommended age | 13 - 18 years |
| File information | docx, 2 pages, 445 KB |
There are no comments yet, write one yourself!

| Downloads count | 4 |
| Resource type | Worksheet |
| Recommended age | 13 - 18 years |
| File information | pdf, 3 pages, 432 KB |
There are no comments yet, write one yourself!





| Resource type | Lesson |
| Recommended age | 15 - 18 years |
| File information | pptx, 11 pages, 1.78 MB |
There are no comments yet, write one yourself!




| Downloads count | 1 |
| Resource type | Lesson |
| Recommended age | 15 - 18 years |
| File information | pptx, 11 pages, 1.71 MB |
There are no comments yet, write one yourself!
| Resource type | Worksheet |
| Recommended age | 15 - 18 years |
| File information | DOC, 4 pages, 142 KB |
There are no comments yet, write one yourself!


| Resource type | Assessment |
| Recommended age | 15 - 18 years |
| File information | DOC, 6 pages, 23.1 KB |
There are no comments yet, write one yourself!




| Downloads count | 14 |
| Resource type | Worksheet |
| Recommended age | 16 - 17 years |
| File information | docx, 8 pages, 468 KB |
There are no comments yet, write one yourself!

| Downloads count | 25 |
| Resource type | Worksheet |
| Recommended age | 15 - 17 years |
| File information | docx, 1 pages, 20.6 KB |
There are no comments yet, write one yourself!

| Downloads count | 1 |
| Resource type | Lesson |
| Recommended age | 15 - 18 years |
| File information | pptx, 9 pages, 1.08 MB |
There are no comments yet, write one yourself!
There are no comments yet, write one yourself!