¡Trabaja con tus estudiantes sobre el DÍA MUNDIAL DEL MEDIO AMBIENTE! 🌱 🌎 

Guía de síntesis en formato word editable 6° año "Diagramas y gráficos". La guía contiene 2 páginas divididas en 2 para trabajar, incluye breve definición  de los contenidos a tratar con los siguientes ejercicios:
-Construir diagrama de tallo y hoja con datos dados.
- Leer, comprender y responder preguntas de gráfico de líneas dobles.
- Completar tabla (porcentaje y ángulo) y crear gráfico circular de acuerdo a datos entregados.
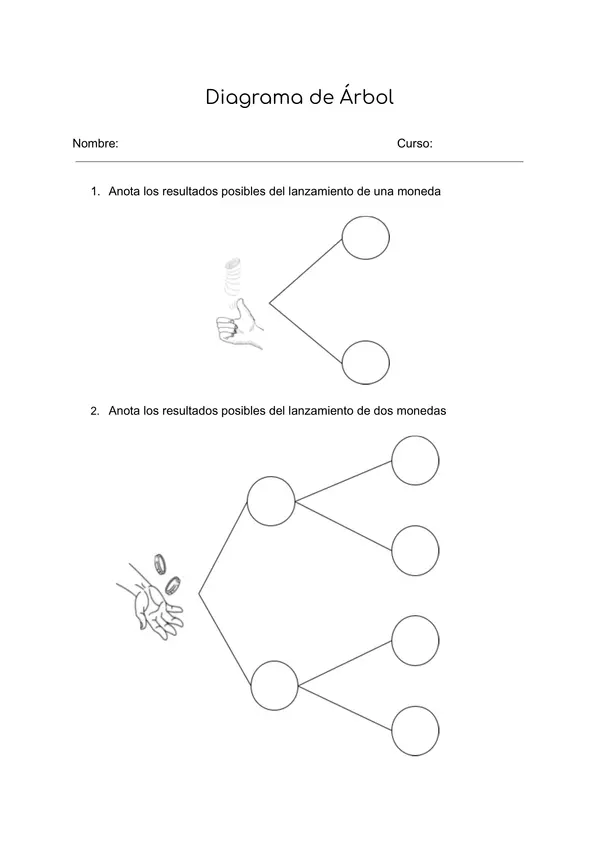
- Crear diagrama de árbol de acuerdo a información dada.
-
-

Aquí les dejo una breve guía para el inicio de las probabilidades en niños y niñas de 5to básico. La idea es que por medio del diagrama del árbol comprendan cómo van aumentando los resultados posibles de un experimento aleatorio al aumentar el número de monedas, dados, u objetos a utilizar y luego puedan descubrir el espacio muestral de cualquier experimento aleatorio. 

Estructura:

I. Componentes (factor, producto)
II. Concepto (suma iterada)
III. Representaciones (grupos y elemento, matrices, diagrama de árbol)
IV. Introducción a la Tabla pitagórica
V. Patrones en las tablas de multiplicar.
VI. Propiedad conmutativa y propiedad distributiva.
VII. Algoritmo de la multiplicación (hasta 99 · 9) 
VIII. Análisis de errores en el algoritmo
IX. Resolución de problemas

Tiene elementos que pueden utilizarse hasta sexto, en mi opinión.

Como siempre, se agradece señalar cualquier error.

El Material que se comparte es para OCTAVO Basico, SUBSECTOR MATEMATICAS
Unidad 4: Mediciones, Trabajo con los conceptos de medidas de posición, percentiles y cuartiles y representación de los datos, utilizando varios tipos de gráficos.
TRAE VIDEO EDUCATIVO DE DIAGRAMA DE ARBOL EN ULTIMA DIAPOSITIVA
SALUDOS CORDIALES 

El Material que se comparte es para OCTAVO Basico, SUBSECTOR MATEMATICAS
Unidad 4: Mediciones, Trabajo con los conceptos de medidas de posición, percentiles y cuartiles y representación de los datos, utilizando varios tipos de gráficos.

SALUDOS CORDIALES 

Determinar la probabilidad de eventos compuestos utilizando el diagrama de árbol es crucial para visualizar todas las posibles combinaciones de resultados y sus probabilidades correspondientes. Esta herramienta permite descomponer un problema complejo en pasos más sencillos, facilitando el cálculo de la probabilidad total de eventos independientes o dependientes. Ayuda a evitar errores, clarifica el proceso de toma de decisiones, y es útil en campos como la estadística, finanzas y ciencias. El diagrama de árbol, al mostrar cada rama y su probabilidad, proporciona una representación clara y estructurada de los eventos compuestos.

Determinar la probabilidad de un evento compuesto es crucial para predecir resultados en situaciones complejas. Utilizar el diagrama de árbol facilita la visualización de todas las posibles combinaciones y sus probabilidades asociadas, asegurando un análisis detallado y preciso. Calcular directamente permite obtener resultados rápidos y eficientes, esenciales en la toma de decisiones informadas. Ambas técnicas son fundamentales en campos como la estadística, economía, y ciencias, mejorando la comprensión de eventos interrelacionados y optimizando estrategias basadas en datos probabilísticos.

La probabilidad de un evento compuesto es crucial en la toma de decisiones y análisis de riesgos, ya que permite calcular la probabilidad de múltiples eventos sucediendo conjuntamente. Utilizando un diagrama de árbol, se desglosan todos los posibles resultados y sus probabilidades, lo cual facilita la visualización y el cálculo preciso de la probabilidad total. Calcular directamente, por otro lado, implica el uso de reglas de probabilidad, como la multiplicación de probabilidades de eventos independientes. Ambas técnicas son esenciales en campos como la estadística, finanzas y ciencias, para modelar y predecir escenarios complejos.

Esta presentación de describir el espacio muestral, contiene objetivo, ejemplos, definiciones y escala de emociones, se explica el diagrama de árbol.
Objetivo: Describir el espacio muestral de un experimento aleatorio.

Esta presentación introduce los conceptos fundamentales de la probabilidad clásica, incluyendo experimentos aleatorios y determinísticos, la regla de Laplace y herramientas como el diagrama de árbol. Es ideal para clases de matemáticas, estadística y probabilidad aplicada.