Curso : Cuarto Año Básico
Unidad : 3. Medimos y calculamos.
| OBJETIVO(S) DE LA CLASE
| · Conocer el transportador ( · Identificar ángulos de 90° y 180° en el entorno
| Objetivo(s) de Aprendizaje: | · Construir ángulos con el transportador y compararlos (OA 19))
| Actitudes: | · Manifestar curiosidad e interés por el aprendizaje de las matemáticas.)
| Habilidades: | · Transferir una situación de un nivel de representación a otro (por ejemplo: de lo concreto a lo pictórico y de lo pictórico a lo simbólico, y viceversa) (OA n))
______________________________________________________________________________________
Inicio:
· El docente saluda cordialmente a la clase
· Se mencionan las normas de trabajo en el aula y de cuidado con el material si procede.
· ¿Qué hicimos la clase anterior? (se escuchan los comentarios de los estudiantes. Se les pide que den ejemplos y que utilicen la pizarra para explicarlos si procede).
· Se da a conocer el objetivo de la clase y se anotan las palabras claves de la clase: medir, transportar, ángulos.
· Estas palabras debe ser usadas al comunicar sus ideas, descubrimientos o procedimientos.
Desarrollo:
· No se usará guía para esta clase.
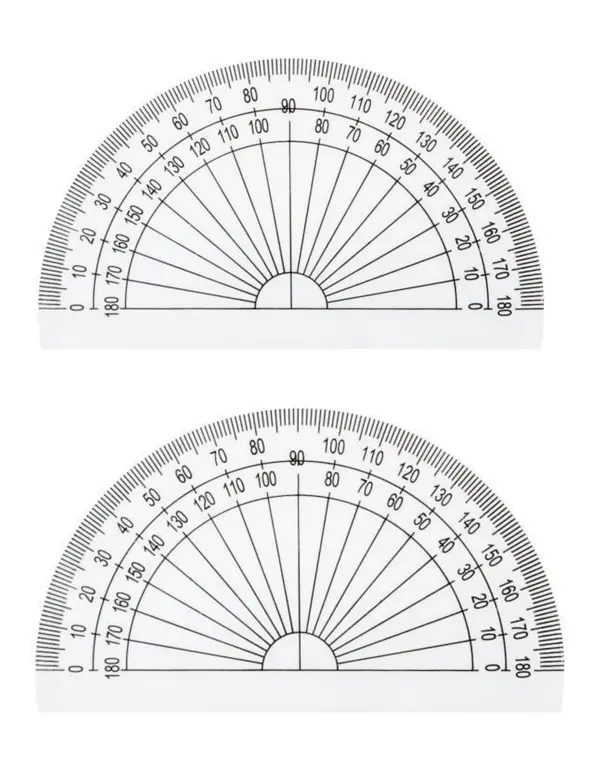
· Se construye el transportador casero y se mide con el todos los elementos del entorno que sea posible, identificando primero todos aquellos que puedan tener forma de ángulo de 90° y después los de 180°.
· Se comentan en grupo los hallazgos.
· Se dibujan los elementos medidos en el cuaderno o pizarra.
Cierre:
· ¿Qué hicimos hoy? (se escucha el resumen de la clase por parte de los estudiantes)
· Se realizan las preguntas o comentarios que se crean necesarios según los acontecimientos sucedidos durante la clase
· ¿Cuál era el objetivo de la clase?
· ¿Lo conseguimos? ¿por qué? Se dan ejemplos.
|
Otro(s) Indicador(es) de Calidad:
· Clima de convivencia escolar: el/la docente fomenta un clima de aula positivo, caracterizado por incentivar el respeto hacia las opiniones de otros (por ejemplo: respetar turnos para hablar, tolerar las diferentes ideas u opiniones expuestas por otros, evitar y rechazar lenguaje violento o soez, entre otros) y a la participación en general del curso. Así también se invita a manifestar preocupación genuina por las dificultades que otros compañeros puedan presentar respecto a su trabajo escolar, ofreciendo su apoyo y sugerencias prácticas para un mejor desempeño.
Recomendaciones:
ü Durante el trabajo colaborativo el/la docente debe monitorear el quehacer de los estudiantes y realizar las preguntas necesarias que le permitan a los estudiantes comunicar y argumentar qué están haciendo, cómo lo están haciendo y para qué lo están haciendo.
Materiales / Recursos:
ü 2 tiras semitransparentes (tapas de carpetas, micas u otros), 1 tornillo de mariposa (por alumnos).
ü Se pueden cambiar los materiales de acuerdo a los recursos con los que se cuenten. Incluso, a elección del docente, pueden usar el transportador simple.
ppt con ejemplos de angulos y actividad propuesta






















There are no comments yet, write one yourself!