CONTENIDOS

1.     Introducción Objeto de la Geometría Analítica

2.     Formula Punto Medio de un segmento 

3.     Formula Distancia entre dos puntos de un segmento

4.     Ejercicios Resueltos

Nota: Se espera de los estudiantes que apliquen conocimientos básicos de potencias y raíces, en el aprendizaje de estos contenidos.
también que sus resultados en la mayoría de los casos puedan verificarse por medio de Gráficas en Geogebra

Hola
Esta presentación la puedes poner en tu clase de matemáticas a tus alumnos, viene acerca del tema de elipse explicacion, un ejemplo, también una conclusión al final en total son once dispositivas.

El material de evaluación está diseñado para evaluar la comprensión y aplicación de conceptos fundamentales de geometría analítica y homotecia en alumnos de III° Medio. La evaluación se divide en dos partes principales: una sección de selección única y otra de desarrollo.

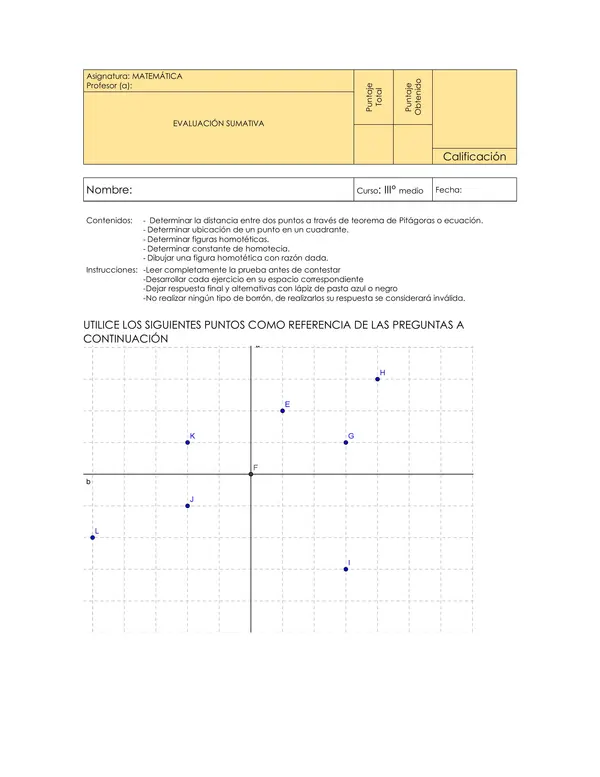
En la sección de selección única, los alumnos deben elegir la respuesta correcta entre varias alternativas. Las preguntas abarcan temas como la identificación de puntos en diferentes cuadrantes del plano cartesiano, la determinación de coordenadas que cumplen condiciones específicas (por ejemplo, pertenecer a un eje u origen), y el cálculo de la distancia entre puntos usando el teorema de Pitágoras. Ejemplos de estas preguntas incluyen determinar las coordenadas de puntos medios y calcular distancias entre diversos puntos.

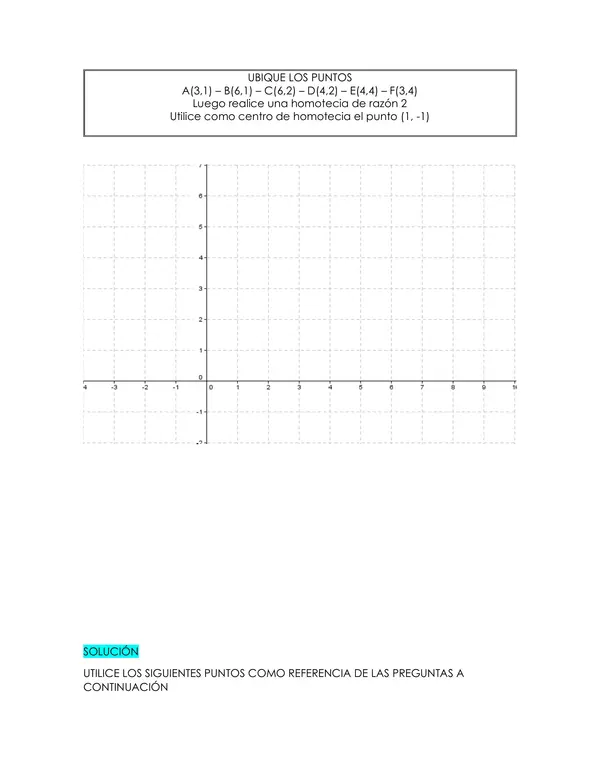
En la sección de desarrollo, los alumnos deben ubicar puntos en un plano cartesiano y realizar una homotecia con una razón dada, utilizando un centro de homotecia específico. Esta parte de la evaluación requiere que los alumnos dibujen y calculen con precisión, demostrando su habilidad para aplicar transformaciones geométricas y sus conocimientos sobre razones y proporciones.

El trabajo del alumno consiste en:

Esta evaluación no solo mide el conocimiento teórico, sino también la capacidad práctica de aplicar conceptos matemáticos en problemas geométricos concretos.

Contenidos 

Geometría Analitica - Nivel Básico

1. Introducción
2. Recordatorio
3. Rectas paralelas
4. Rectas perpendiculares
5. Problemas Resuelto

Nota :

Los conceptos de rectas paralelas y de rectas perpendiculares (nivel de secundaria). Para poder comprender y resolver los problemas, el alumno necesitará tener las siguientes destrezas:Saber interpretar o representar en el plano la gráfica de una recta.Saber encontrar la ecuación de la recta que pasa por dos puntos.Resolver ecuaciones de primer grado.

Se sugiere que el estudiante se familiarice con las herramientas de construcción gráfica de Gogebra.

Contenidos.

Geometría, Elementos Básicos del Triángulo. 
Clasificación según sus Lados y Ángulos

1. Definición, lados, vértices y ángulos
2. Altura, base, mediana, bisectriz, ortocentro, baricentro e incentro
Clasificación de Triángulos:
3. Según los ángulos: rectángulo y oblicuángulo
4. Según los lados: equilátero, isósceles y escaleno
5.Ejercicios Resueltos

Nota: es importante que el estudiante comprenda la importancia de estos conceptos y propiedades. Podrá más adelante transferir y avanzar en nuevos conocimientos, Geometría Analítica y Trigonometría.

 El plano cartesiano es un sistema de coordenadas bidimensional utilizado en matemáticas y ciencias para representar puntos, líneas, y figuras geométricas en un espacio de dos dimensiones. Es fundamental para la geometría analítica y el análisis de funciones. 

Clases de Física y Matemáticas aplicadas, para las Ciencias y la Ingeniería, a Domicilio, Presenciales online (Zoom).

*) aclaración de los conceptos, 
*) formulación de problemas, 
*) investigación de cómo implementar una solución a un problema específico (incluyendo sistemas abiertos y cerrados), 
*) solución de los problemas y entrega de informes, 
*) programación de un archivo que ejecute los análisis deseados en MS Excel 

¡Contacte me sin compromiso alguno, para averiguar cómo le puedo asistir!. Seleccione de la siguiente lista el campo más cercano a su problema para que pueda poner me en contacto con Usted lo mas pronto posible.

*) Álgebra general
*) Álgebra lineal
*) Trigonometría
*) Geometría analítica
*) Cálculo de una variable
*) Cálculo de dos o más variables
*) Cálculo vectorial
*) Cálculo tensorial
*) Métodos numéricos
*) Cálculo varacional
*) Variable compleja
*) Ecuaciones Diferenciales Ordinarias 
*) Ecuaciones Diferenciales Parciales
*) Ecuaciones Integrales Lineales
*) Cálculo Espinorial
*) Topología 
*) Probabilidad y Estadística aplicada
*) Solución de problemas de física para ingeniería

Tenga la seguridad que mis servicios son los más competitivos y profesionales especializados en el campo de la fisica-matemática.

Calcular el área de paralelogramos es fundamental en geometría, ya que permite comprender mejor las propiedades y aplicaciones de estas figuras en diversas áreas. Utilizar diferentes estrategias, como la fórmula base por altura o el descomponer el paralelogramo en triángulos, enriquece la comprensión y flexibilidad para resolver problemas. Estas técnicas también facilitan la aplicación en contextos reales, como diseño y construcción, optimizando el uso de materiales y espacios. Además, dominar varias estrategias desarrolla habilidades analíticas y fomenta el pensamiento crítico, esenciales en matemáticas y ciencias.

Calcular el área de trapecios utilizando diferentes estrategias es fundamental para entender la versatilidad de las matemáticas en problemas reales. Aplicar métodos diversos, como fórmulas directas o descomposición en figuras más simples, permite a los estudiantes y profesionales adaptarse a diferentes contextos y necesidades. Además, promueve el desarrollo de habilidades analíticas y la capacidad de resolver problemas de manera eficiente. Esta flexibilidad es clave para aplicaciones prácticas en áreas como la ingeniería, la arquitectura y la planificación, donde los trapecios a menudo aparecen en diseños y cálculos.

Los polígonos y poliedros son figuras fundamentales en la geometría. Los polígonos, figuras planas con lados rectos, y los poliedros, sus contrapartes tridimensionales, son esenciales en diversas aplicaciones, desde el diseño arquitectónico hasta la modelización en ciencias. La intersección de rectas, por otro lado, es clave para determinar puntos de corte, resolver sistemas de ecuaciones lineales y analizar relaciones geométricas y espaciales. Comprender estas estructuras y conceptos es crucial para el desarrollo de habilidades analíticas y de resolución de problemas en matemáticas y otras disciplinas.