📖 ¡Recursos para celebrar el Día de los Trabajadores! 👩‍🏫 👨‍🔧 

Ficha de actividades para alumnos de básica, en la que deberán clasificar formas dimensionales y tridimensionales según lo indicado.
Clasificar es ordenar diversos elementos utilizando un criterio común.  Todo esto es fundamental para construir un nuevo concepto.

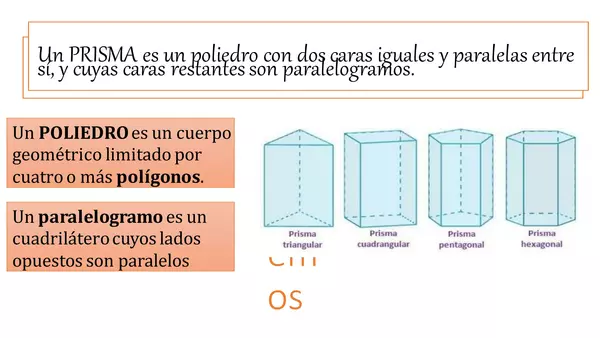
Un prisma pentagonal es un sólido tridimensional con una base pentagonal y caras laterales que son rectángulos o paralelogramos. La base es un pentágono, una figura de cinco lados, y las caras laterales se conectan a los lados de la base. Estas caras laterales son rectángulos si el prisma es un prisma recto, o pueden ser paralelogramos si el prisma no es recto. Cada prisma pentagonal tiene cinco vértices en la base y otros cinco en la parte superior donde las caras laterales se encuentran.

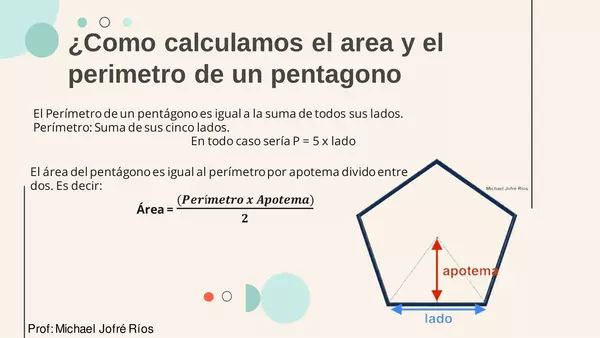
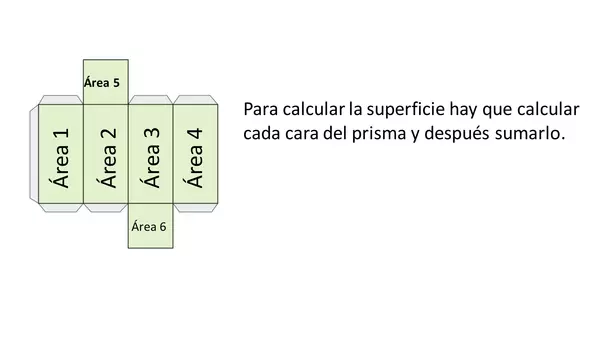
Para calcular el área de la superficie de un prisma pentagonal, primero debes encontrar el área de la base pentagonal. Esto se hace utilizando la fórmula del área del pentágono. Luego, debes encontrar el área de las cinco caras laterales y sumarlas. La fórmula general del área de la superficie de un prisma pentagonal es:

Área de la superficie = Área de la base + 5 × Área de una cara lateral

El volumen de un prisma pentagonal se calcula multiplicando el área de la base pentagonal por la altura del prisma. La fórmula general es:

Volumen = Área de la base × Altura

Calcular el área de la base pentagonal puede ser un poco más complicado que en el caso de un triángulo o un cuadrado, ya que implica trigonometría y ángulos. La altura del prisma es la distancia perpendicular desde la base hasta la cara opuesta.

Los prismas pentagonales tienen aplicaciones en la geometría, la arquitectura y la ingeniería cuando se trabajan con estructuras que tienen bases pentagonales. Su estudio permite calcular áreas y volúmenes en situaciones específicas que involucran esta forma geométrica única. En resumen, un prisma pentagonal es un sólido tridimensional con una base pentagonal y caras laterales que se utilizan para calcular áreas y volúmenes en contextos matemáticos y prácticos.

Los poliedros son figuras geométricas tridimensionales formadas por polígonos. Su estudio es fundamental en matemáticas y arquitectura, ya que permiten entender la estructura y forma de objetos en el espacio. Los poliedros regulares, como el cubo y el tetraedro, tienen aplicaciones en cristalografía, química y biología. Además, su análisis fomenta el pensamiento espacial y la resolución de problemas, habilidades esenciales en diversas disciplinas científicas y tecnológicas. Conocer los poliedros ayuda a comprender mejor el mundo físico y las propiedades geométricas de los objetos que nos rodean.

 Esta actividad  permite a los estudiantes crear figuras geométricas tridimensionales de manera sencilla y divertida. Consiste en una serie de plantillas descargables que incluyen diferentes figuras, como cubos, pirámides y prismas. Cada plantilla está diseñada con líneas de corte y pliegue, facilitando su armado.

Esta actividad es ideal para clases de matemáticas o manualidades y se puede realizar de forma individual o en grupos, promoviendo el aprendizaje colaborativo. ¡Una forma práctica y visual de entender la geometría!
¡Espero les guste!

Objetivo: Conocer la superficie y volumen de los prismas de base Triangular.

Un prisma triangular es un sólido tridimensional con una base en forma de triángulo y tres caras laterales rectangulares o paralelogramos que se conectan a los vértices de la base. Tiene cinco vértices en total, tres en la base y dos en la parte superior donde las caras laterales se encuentran. Los prismas triangulares pueden tener bases de triángulos equiláteros, isósceles o escalenos, y la altura es la distancia perpendicular desde la base hasta la cara opuesta.

Para calcular el área de superficie de un prisma triangular, se suma el área de la base triangular al doble del área de una de las caras laterales. La fórmula general es Área de la superficie = Área de la base + 2 × Área de una cara lateral.

El volumen de un prisma triangular se calcula multiplicando el área de la base triangular por la altura del prisma. La fórmula general es Volumen = Área de la base × Altura.

Estos prismas se encuentran en diversas aplicaciones, desde la geometría y la matemática hasta la arquitectura y la ingeniería. Su estudio permite calcular áreas y volúmenes en situaciones prácticas. En resumen, un prisma triangular es un sólido geométrico con una base triangular y tres caras laterales que se utiliza para calcular áreas y volúmenes en una variedad de contextos matemáticos y prácticos.

En esta clase veremos que los vectores son segmentos de una línea recta que están orientados dentro de un plano bidimensional o tridimensional, también conocido como un espacio vectorial. se incluyen ejercicios para explicaren clase y actividades para que nuestros alumnos practiquen. 

Esta guía educativa está diseñada para ayudar a los estudiantes de primaria a comprender y diferenciar entre figuras bidimensionales (2D) y tridimensionales (3D). A través de explicaciones claras, ilustraciones coloridas y diversas actividades, los estudiantes aprenderán a identificar, clasificar y describir diversas figuras geométricas, desarrollando una base sólida en geometría. 

Esta guía de laboratorio de Matemática para Cuartos Básicos tiene como objetivo que los estudiantes comprendan y midan el volumen de cuerpos tridimensionales (figuras 3D). A través de la práctica con jarros graduados y vasos de precipitados, los estudiantes estiman y verifican el volumen de objetos irregulares, relacionando el concepto de volumen con la capacidad de los recipientes. La guía incluye predicciones iniciales sobre el volumen de diferentes objetos y proporciona una tabla para registrar los resultados obtenidos en el experimento, facilitando la comprensión del volumen en unidades como mililitros (ml) y centímetros cúbicos (cm³).

 Demostrar comprensión de las narraciones leídas: › extrayendo información explícita e implícita › reconstruyendo la secuencia de las acciones en la historia › identificando y describiendo las características físicas y sentimientos de los distintos personajes › recreando, a través de distintas expresiones (dibujos, modelos tridimensionales u otras), el ambiente en el que ocurre la acción › estableciendo relaciones entre el texto y sus propias experiencias › emitiendo una opinión sobre un aspecto de la lectura. 

La papiroflexia, también conocida como el arte del origami, implica la creación de objetos tridimensionales a partir de papel mediante el plegado de una hoja. Esta práctica puede ser una herramienta efectiva en el desarrollo de la habilidad espacial y visual, ya que requiere una comprensión clara de la geometría tridimensional y la capacidad para visualizar objetos en diferentes ángulos y perspectivas.

La práctica regular del origami puede mejorar la habilidad espacial y visual de una persona, ya que implica el uso de habilidades como la percepción visual, la memoria espacial, la imaginación y la creatividad. Los practicantes de origami deben ser capaces de visualizar mentalmente cómo un objeto de papel se verá una vez que se complete, lo que les permite planificar cuidadosamente los pliegues y la forma final.

Además, el origami también puede mejorar la coordinación mano-ojo, ya que requiere la manipulación precisa de pequeñas piezas de papel.