ProfeCoins 
8
8| Tipo de recurso | Guía de trabajo |
| Edad recomendada | 15 - 18 años |
| Info. del archivo | DOC, 4 páginas, 142 KB |
El material proporcionado se enfoca en enseñar a los estudiantes de III° medio cómo expresar números complejos en su forma polar. La guía está estructurada de manera clara y didáctica, cubriendo los conceptos esenciales y proporcionando ejemplos prácticos para asegurar la comprensión del contenido.
- introducción a la Forma Polar de los Números Complejos:
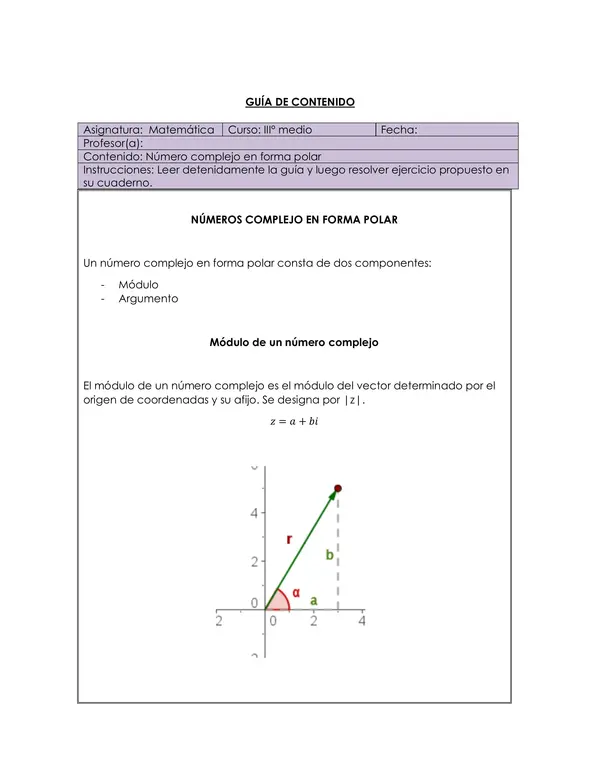
- Módulo de un Número Complejo:
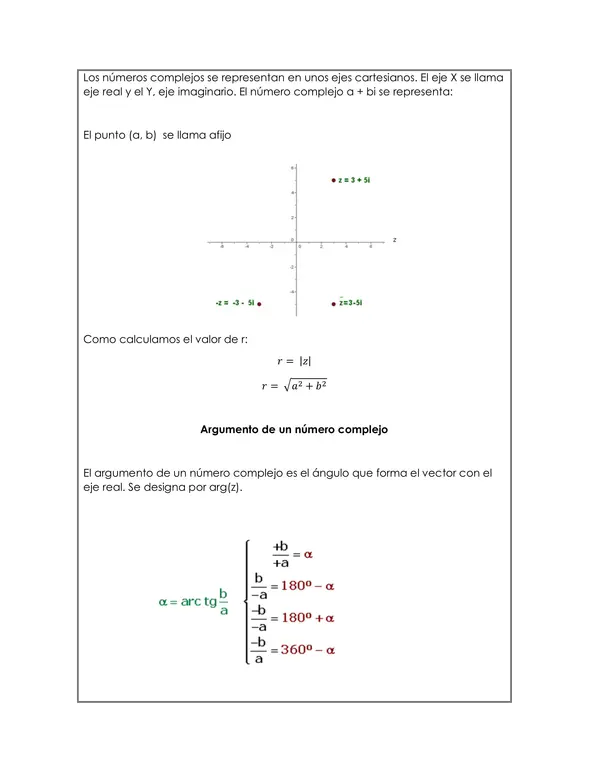
- Representación en Ejes Cartesianos: Se explica cómo los números complejos se representan en un plano cartesiano, con el eje real y el eje imaginario, y se define el afijo del punto.
- Argumento de un Número Complejo:
-
Definición del Argumento: El argumento de un número complejo es el ángulo que forma el vector con el eje real, designado como
arg(𝑧)=𝛼arg(z)=α. -
Expresión de un Número Complejo en Forma Polar:
El alumno debe leer y entender detenidamente la guía, siguiendo cada paso y fórmula presentada. Luego, debe aplicar los conocimientos adquiridos para resolver el ejercicio propuesto. Este ejercicio consiste en convertir un número complejo dado a su forma polar, calculando tanto el módulo como el argumento y expresando el resultado final en la forma polar. Este trabajo permitirá al alumno practicar y consolidar su comprensión sobre la representación de números complejos en el plano cartesiano y su conversión a forma polar, una habilidad fundamental en matemáticas avanzadas.
No hay comentarios aún, ¡escribe uno!